Prolog clp(fd) solve killer sudoku and greater killer sudoku
Solving standard sudoku using SWI-Prolog clpfd
In the manual of clpfd of SWI-Prolog, there is already an example of using the clpfd to solve the puzzle Sudoku. It really show the power of Prolog’s constraint programming to solve hard problem with a bunch of lines of code. But recently, I find out that there are a lot of variants of Sudoku. So I would like to show how can we add very small modification to the Sudoku solver to solve this problem in Prolog very easily.
Killer Sudoku & Greater Killer Sudoku Problem Definition
Killer Sudoku is a famous variant of standard Sudoku. In additional to the standard Sudoku rules, a Killer Sudoku is divided into cages, the sum of the numbers in a cages must equal the small number in the left corner, and same number can not appear in a cage more than once. The Killer Sudoku is a combination of Sudoku and Kakuro.
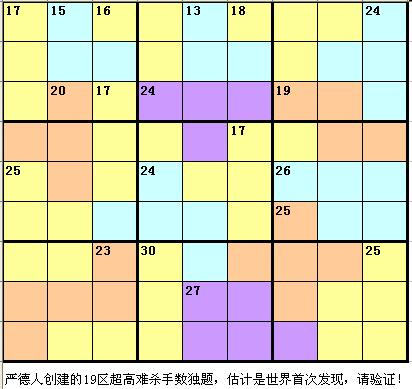
Greater Killer Sudoku combines the rule of Killer Sudoku and Comparison Sudoku, and has sum relation for some of the cages instead of the sum information. An example of Greater Killer Sudoku can be show as the following image from daily killer sudoku.
Solving Killer Sudoku
To solve the Killer Sudoku, we just need to add the cages’ constraints to the solver, when we define the problem, we also give the cages’ information and their corresponding sum.
The whole program is something like the following.
get_value_by_key([], _, _) :- !.
get_value_by_key([X-Y|_], X, Y) :- !.
get_value_by_key([Z-_|Ps], X, Y) :- Z \= X, get_value_by_key(Ps, X, Y).
region_constrain(Sums, X-Vs) :-
get_value_by_key(Sums, X, Value),
all_distinct(Vs),
sum(Vs, #=, Value).
killer_sudoku(Rows, Splits, Sums) :-
length(Rows, 9), maplist(same_length(Rows), Rows),
length(Splits, 9), maplist(same_length(Splits), Splits),
append(Rows, Vs), Vs ins 1..9,
append(Splits, Ks),
pairs_keys_values(Pairs, Ks, Vs),
sort(1, @>=, Pairs, SortedPairs),
group_pairs_by_key(SortedPairs, Regions),
maplist(all_distinct, Rows),
transpose(Rows, Columns),
maplist(all_distinct, Columns),
Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
blocks(As, Bs, Cs),blocks(Ds, Es, Fs),blocks(Gs, Hs, Is),
maplist(region_constrain(Sums), Regions).
So we only need to pass the additional cages’ information and their corresponding sum information, and build the constraint relation for them. It is only around 10 lines more code than the standard Sudoku solver, and we can already solve every killer sudoku in Prolog now.
And also we should notice, despite it’s name, Killer Sudoku’s difficult levels varies, simple Killer Sudoku may even be simpler than normal Sudoku, but the hardest one may take hours even days to crack.
So I do some test to solve various Killer Sudoku I found from online, and see how well the solver can tackle the problems.
For the problem from wiki, it solve the problem instantly, but for some harder problems, it may take minutes even hours to solve.
?- problem(wiki, Rows, Splits, Sums), killer_sudoku(Rows, Splits, Sums),
| append(Rows, Vs), time(label(Vs)), maplist(portray_clause, Rows).
% 591 inferences, 0.000 CPU in 0.000 seconds (98% CPU, 17776040 Lips)
[2, 1, 5, 6, 4, 7, 3, 9, 8].
[3, 6, 8, 9, 5, 2, 1, 7, 4].
[7, 9, 4, 3, 8, 1, 6, 5, 2].
[5, 8, 6, 2, 7, 4, 9, 3, 1].
[1, 4, 2, 5, 9, 3, 8, 6, 7].
[9, 7, 3, 8, 1, 6, 4, 2, 5].
[8, 2, 1, 7, 3, 9, 5, 4, 6].
[6, 5, 9, 4, 2, 8, 7, 1, 3].
[4, 3, 7, 1, 6, 5, 2, 8, 9].
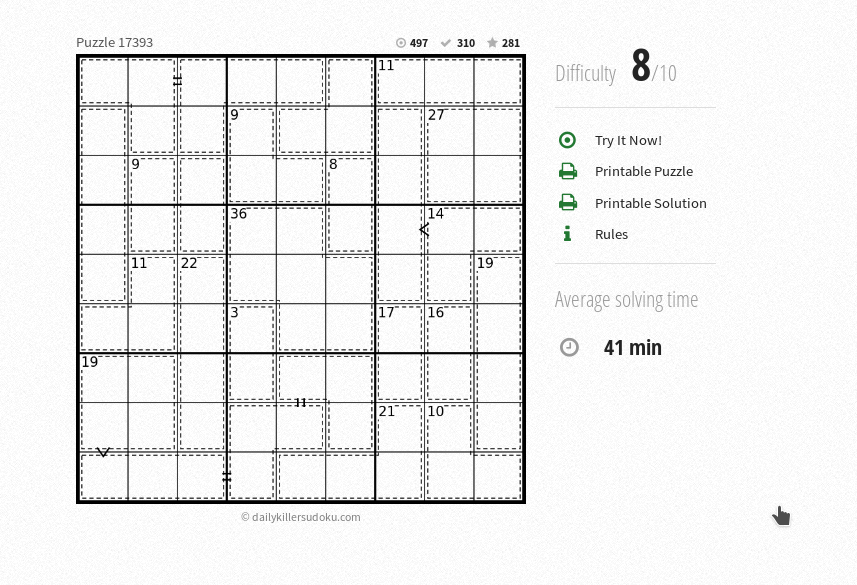
Difficulty level 10/10 Killer Sudoku from the daily killer sudoku website. It toke around 2 minutes to find the solution, and take around 6 minutes to prove that there is on other solutions. Since it is marked as the most difficult Killer Sudoku on the website, I think the speed is already quite fast. On the website, it said the average time to solve the problem is 44 minutes, but it may because you can use hint for the task for simple problem(difficult level 1/10), the average time is also around 40 minutes, so it is likely either all the people who try to solve the difficult one are expert at solving Killer Sudoku or the time is not actually reflected the difficult level of the problem(like people want to use hint when they stuck).
?- problem(daily_killer_sudoku_hard, Rows, Splits, Sums), killer_sudoku(Rows, Splits, Sums),
| append(Rows, Vs), time(label(Vs)), maplist(portray_clause, Rows).
% 277,532,279 inferences, 112.211 CPU in 112.575 seconds (100% CPU, 2473301 Lips)
[2, 9, 6, 7, 1, 3, 4, 8, 5].
[3, 7, 5, 2, 4, 8, 1, 9, 6].
[1, 4, 8, 5, 6, 9, 3, 7, 2].
[8, 5, 3, 9, 7, 1, 2, 6, 4].
[9, 6, 1, 3, 2, 4, 7, 5, 8].
[4, 2, 7, 8, 5, 6, 9, 1, 3].
[6, 3, 2, 1, 9, 5, 8, 4, 7].
[5, 8, 9, 4, 3, 7, 6, 2, 1].
[7, 1, 4, 6, 8, 2, 5, 3, 9].
% 906,040,567 inferences, 382.551 CPU in 384.761 seconds (99% CPU, 2368417 Lips)
false.
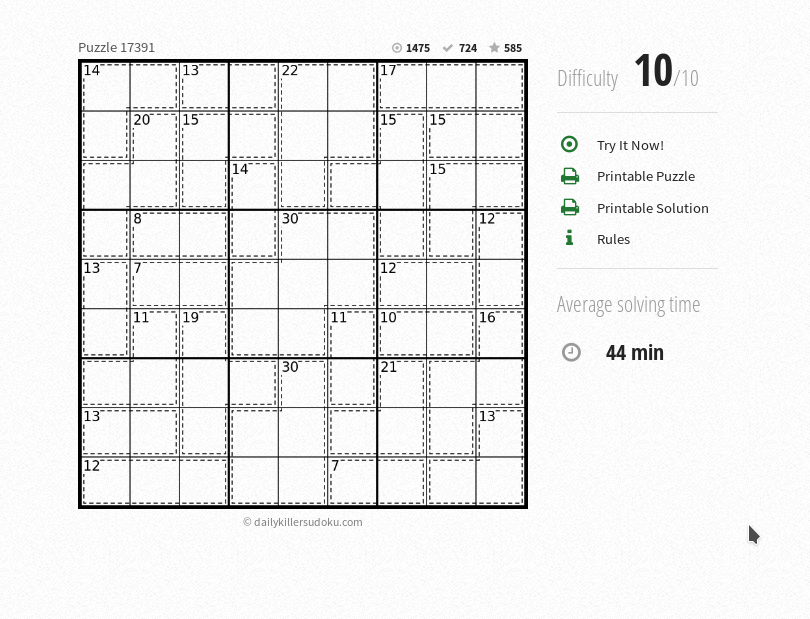
Then I coincidentally encountered a page said that there is a most difficult 19 cages Killer Sudoku in the world. Although I do not think there is a objective standard for difficulty, but it seems to be quite difficult since every cage is not limited to one block which make simple strategy for solving Killer Sudoku not working. And in the post, the author said it take him six days to solve the problem. So I decide to give it a try to the constraint solver.
It actually take quite long to solve the problem(around 12h to get the solution). But since except the definition constraints of the problem, I do not use any other advanced strategy, I think the speed is already satisfactory.
?- problem(most_difficult_killer_sudoku, Rows, Splits, Sums), killer_sudoku(Rows, Splits, Sums),
| append(Rows, Vs), time(label(Vs)), maplist(portray_clause, Rows).
% 98,413,615,883 inferences, 43078.045 CPU in 43212.116 seconds (100% CPU, 2284542 Lips)
[9, 2, 8, 3, 4, 7, 6, 1, 5].
[3, 6, 7, 5, 1, 8, 4, 9, 2].
[5, 1, 4, 6, 2, 9, 7, 3, 8].
[2, 8, 3, 9, 7, 6, 1, 5, 4].
[7, 9, 1, 4, 3, 5, 2, 8, 6].
[4, 5, 6, 1, 8, 2, 9, 7, 3].
[6, 3, 2, 7, 5, 1, 8, 4, 9].
[8, 7, 5, 2, 9, 4, 3, 6, 1].
[1, 4, 9, 8, 6, 3, 5, 2, 7].
Solving Greater Killer Sudoku
To solve the Greater Killer Sudoku, we just need to add the comparison constraint relation to the solver. And we should also notice that some of cages do not have sum information, so when build the constraint for sum information, we should only select the area with sum information. The program is like following.
compare_constrain(Regions, [X, Y]-Relation) :-
get_value_by_key(Regions, X, Xs),
get_value_by_key(Regions, Y, Ys),
all_distinct(Xs), all_distinct(Ys),
sum(Xs, #=, Vx),
sum(Ys, #=, Vy),
(Relation = less
-> Vx #< Vy
; ( Relation = equal
-> Vx #= Vy
; Vx #> Vy
)
).
has_sum_info(Pos, X-_) :- member(X, Pos).
greater_killer_sudoku(Rows, Splits, Sums, Compares) :-
length(Rows, 9), maplist(same_length(Rows), Rows),
length(Splits, 9), maplist(same_length(Splits), Splits),
append(Rows, Vs), Vs ins 1..9,
append(Splits, Ks),
pairs_keys_values(Pairs, Ks, Vs),
sort(1, @>=, Pairs, SortedPairs),
group_pairs_by_key(SortedPairs, Regions),
maplist(all_distinct, Rows),
transpose(Rows, Columns),
maplist(all_distinct, Columns),
Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
blocks(As, Bs, Cs),blocks(Ds, Es, Fs),blocks(Gs, Hs, Is),
maplist(compare_constrain(Regions), Compares),
pairs_keys(Sums, PosHasSumValue),
pairs_values(Regions, Vss),
maplist(all_distinct, Vss),
include(has_sum_info(PosHasSumValue), Regions, RegionsHasSum),
maplist(region_constrain(Sums), RegionsHasSum).
We define another predicate called compare_constrain which take the regions information
and two cages’ comparison relation. It is something like [a, b]-less which means cage
a’s sum is less than cage b’s sum. And we just add this constraints to the solver. All
the remaining are exactly the same as Killer Sudoku’s solver.
I use the above solver to solve the most difficult greater killer sudoku from the daily killer sudoku as following, and it take much more time to solve the problem (around 5 hours) than the most difficult Killer Sudoku from the website. I think that’s because the compare relations are not very strong constraint and some cages missing the sum constraint information which make the search space for the constraint propagation much much larger than normal Killer Sudoku.
?- problem(daily_greater_killer_sudoku_hard, Rows, Splits, Sums),
| greater_killer_sudoku(Rows, Splits, Sums,
| [[a,b]-equal, [j, o]-less, [r, v]-equal, [u, y]-greater, [y, v]-equal]),
| append(Rows, Vs), time(label(Vs)), maplist(portray_clause, Rows).
% 26,391,594,689 inferences, 17021.320 CPU in 17080.693 seconds (100% CPU, 1550502 Lips)
[5, 4, 2, 9, 6, 8, 7, 3, 1].
[8, 9, 1, 3, 7, 5, 2, 4, 6].
[6, 7, 3, 4, 2, 1, 5, 8, 9].
[9, 2, 8, 5, 4, 7, 1, 6, 3].
[3, 1, 7, 8, 9, 6, 4, 5, 2].
[4, 6, 5, 2, 1, 3, 9, 7, 8].
[7, 3, 6, 1, 5, 2, 8, 9, 4].
[1, 8, 4, 7, 3, 9, 6, 2, 5].
[2, 5, 9, 6, 8, 4, 3, 1, 7].
Conclusion
So the intention of this post is not to build the fastest Killer Sudoku and Greater Killer Sudoku solver, just want to show how we can just add a bunch of lines of code to the standard Sudoku solver in clpfd to get a general solver which can solve Killer Sudoku and Greater Killer Sudoku in a quite reasonable time and to show that clpfd in SWI-Prolog is actually a very good domain specific language at solving such puzzles over integer domain. And the expressiveness of clpfd make the solution very straightforward and less bug prone.
So in general, with only around 20 lines of more code, we can solve two famous extension of normal Sudoku problem in Prolog, and the code is concise and express high level definition of the problem and thus is less bug prone, and can actually solve very difficult problems in a reasonable time :).
You can find the whole program from clpfd-killer-sudoku.
m00nlight 18 November 2018